The Effects of Frequency in High Frequency Welding

As a leading manufacturer for solid state high frequency welder ,we are honored to share our information with all customer.

One of the most important parameters in high frequency pipe and tube welding is the welding frequency. Yet, until recently, it has been one of the most misunderstood!

Because no unified theory describing how frequency affects the weld area was available, most of what was known was based on empirical data and experiment. And because experimenting in a real pipe and tube mill environment is time consuming and difficult, much of the data available was incomplete and contradictory. A comprehensive theory for how frequency affects the high frequency welding process is now availablei and has been validated through experiment and comparison to actual tube welding data from numerous manufacturing operations. This theory describes how welding frequency

affects:

•The Heat Distribution in the area of the weld “Vee”.

•The Weld Power Requirement.

•The Size of the Heat Affected Zone (HAZ).

•The level of Magnetic Flux in the Impeder.

More importantly, the theory identifies the “optimum” welding frequency for a particular tube size, mill speed, and material.

This paper includes a minimum of mathematics with the aim of making it straight

forward for the tube mill engineer to follow. Those interested in the details of the theory and its derivation should consult the paper cited in the end notes.

How the “Vee” Heats to the Forge Weld Temperature:

Let’s consider the typical pipe and tubing, high frequency induction welding

situation where the tube material is much thicker than an “Electrical Reference Depth” and an impeder is used that can support the required level of magnetic flux. This accounts for over 90% of the situations encountered in practice. Empirically, “how” the weld “vee” heats has been understood for a long time. High frequency current in the work coil induces a current in the opposite direction in the unwelded portion of the tube directly under the coil. This part of the process behaves as an electrical transformer in the sense that the portion of tube directly under the coil forms the single turn secondary of the transformer and the current is “stepped up” by the number of turns of the work coil. One of the functions of the impeder in the process is to form the “core” of the transformer. Thus, the magnetic flux that couples the current between the work coil and tube is essentially contained in the impeder. The current induced in the tube must flow in a2 closed electric circuit. When the current reaches the unwelded portion of the tube, a reasonable fraction flows along the “vee” edge to the apex and back closing the circuit with the current flowing around the tube, under the work coil. The current flows along the edge of the “vee” due to two physical phenomena:

• “The Classical Proximity Effect” which states that the magnetic field produced by a

high frequency current flowing in one direction attracts a high frequency current

flowing close to it in the opposite direction. As the high frequency currents on both

sides of the “vee” are flowing in opposite directions, they tend to pull each other into

the weld “vee”.

• The “Surrogate Proximity Effect” in which a high frequency current in the presence of a magnetic field is attracted by the field. The physical laws of high frequency currents show that the equivalent surface current on a conductor equals the magnetic field flowing parallel to its surface. This in fact is the stronger effect in the weld “vee” as the total magnetic flux in the impeder must pass through the weld “vee” to close

around the work coil.

The exact distribution of the current in the “vee” area is described by a set of

physical laws called “Maxwell’s Equations”. The important consequence of these is that

the current density, or the distribution of electric current in the “vee” material, can be

found from:

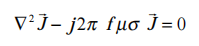
where: J" is the electrical current density in the pipe or tube material,

f is the electrical welding frequency,

σ is the electrical conductivity of the pipe or tube material,

µ is the magnetic permeability of the pipe or tube material.

and j is the square root of -1.

Solution of this equation shows that the current in a high frequency electrical

system flows essentially on the surface of its conductors - the well known “Skin Effect”. The highest concentration of current is at the surface of a conductor and as one moves into the conductor away from the surface, the current density reduces exponentially. The distance into the conductor at which the current density is e-1 or 0.368 times its value at the surface is called the “Electrical Reference Depth” and is determined by solving the equation above:

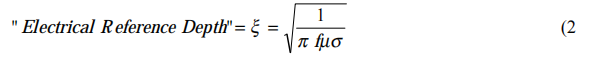
The current flowing in the “vee” dissipates power in the “vee” and causes it to heat. If we consider a tiny volumetric element of “vee” material, the current passing

through it dissipates power in the form of heat due to losses in the electrical resistance ofthe element. Because the volumetric power is proportional to the square of the current density, the heat generated in the “vee” reduces at a rate twice as fast as the current density as one moves from the surface, into the conductor. The “ Electric Power Reference Depth” is then half of the “Electrical Reference Depth”. The heating byelectric power dissipation causes the temperature of the material in the vicinity of the“vee” to rise because of two physical phenomena:

• First, heat generated in the element is stored in its “Heat Capacitance”. It is a well understood physical law that the temperature of a volumetric element equals the heat energy contained in it multiplied by its volumetric Heat Capacity.

• Second, adjacent volumetric elements exchange heat in proportion to their temperature difference. This is the well known process of Thermal Conduction.

Both Heat Capacitance and Thermal Conduction play an important role in heating the “vee”. In the study of Physics, these two effects are simultaneously described by the Biot-Fourier Equation:

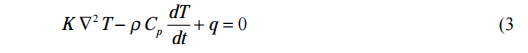
where: T is the temperature distribution in the material,

q is the heat generated in the material,

K is the thermal conductivity of the pipe or tube material,

ρ is the density of the material,

and Cp is the heat capacity of the material.

Solution of this equation tells us that when heat is generated in a portion of a

thermally conducting piece of material, the temperature rise is instantaneously confined to the region being heated. However as time increases, adjacent material elements experience a temperature rise as the heat spreads out due to thermal conduction. The shape of this temperature distribution at any point in time contains a very abrupt transition between a temperature approaching that of the part of the material being heated and that of the material before it was heated. If a single element of material starts to heat at time t = 0, the location of this temperature transition relative to the heated element can be described by the “Thermal Reference Depth” which increases with time:

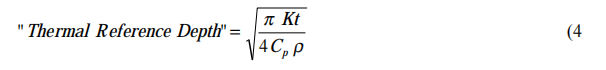
To this point in the paper, everything disclosed about the high frequency welding process has been known for some time. What was not understood until recently was the answer to the question:

Is the high frequency welding process governed by electrical “Skin Effect” so that

the temperature distribution in the “vee” edge is determined by the “Electric

Power Reference Depth” or is it governed by “Thermal Conduction” so that the

temperature distribution is determined by the “Thermal Reference Depth”?

The answer is that the process can be controlled by either the “Electric Power Reference Depth” or the “Thermal Reference Depth” depending on the welding frequency, mill speed, and tube product being produced!! The interaction between electrical “Skin Effect” and “Thermal Conduction” has been determined by combining Maxwell’s Equations with the Biot-Fourier Equation and solving the two together. The result explains the effect of frequency on the induction tube welding process and reconciles the abnormalities between conflicting experimental data.

The Effect of  Frequency on the Power Required to Weld:

The principle result of this new process model is that the power required to heat

the “vee” to the forge welding temperature can be accurately predicted from an equation relating welding frequency, mill speed, “vee” length, tube wall thickness, and the electrical and thermal properties of the strip material. The resulting equation is:

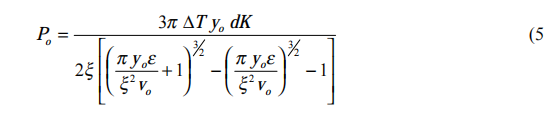
where   Po is the power required in the “vee” to weld the pipe or tube,

d is the wall thickness of the pipe or tube,

vo is the mill speed,

yo is the length of the weld “vee”,

∆T is the forge temperature rise required to weld the material,

and ε equals K /Cp ρ which is the thermal diffusivity of the material.

If you wanna learn more information for high frequency welding machine , please feel free to contact us.